When we talk about mathematical concepts, one that often comes up is "e to the negative infinity." This concept is crucial in various fields, including calculus, statistics, and finance. Understanding this idea not only helps in academic pursuits but also in real-world applications. In this article, we will delve into the intricacies of e to the negative infinity, exploring its mathematical significance and practical uses. By the end of this article, you will have a solid understanding of this concept and how it relates to various domains.
The number "e," approximately equal to 2.71828, is known as Euler's number, named after the Swiss mathematician Leonhard Euler. It is a fundamental constant in mathematics, especially in scenarios involving exponential growth or decay. When we raise "e" to the power of negative infinity, we are essentially examining the behavior of functions as they approach very small values. This article aims to clarify this concept with examples, applications, and relevant mathematical theories.
As we explore "e to the negative infinity," we will break down the topic into manageable sections, providing insights into its definition, calculation, and applications in different fields. Whether you are a student, a professional, or simply a math enthusiast, this comprehensive guide will enhance your understanding of this fundamental concept.
Table of Contents
- What is E?
- Understanding Negative Infinity
- Definition of E to the Negative Infinity
- Mathematical Calculation of E to the Negative Infinity
- Applications in Science
- Financial Applications
- Real World Examples
- Conclusion
What is E?
The number "e" is a mathematical constant that is defined as the limit of (1 + 1/n)^n as n approaches infinity. It is a transcendental number, meaning it cannot be expressed as a simple fraction. Here are some key points about "e":
- Approximate value: 2.71828
- Used in natural logarithms
- Crucial in calculus, particularly in relation to exponential functions
Understanding Negative Infinity
Negative infinity is a concept used in mathematics to describe a value that decreases without bound. In practical terms, it represents the idea of something getting smaller and smaller indefinitely. Here’s a deeper look:
- Symbolically represented as -∞
- Often used in limits and calculus
- Helps in understanding behavior of functions as they approach zero
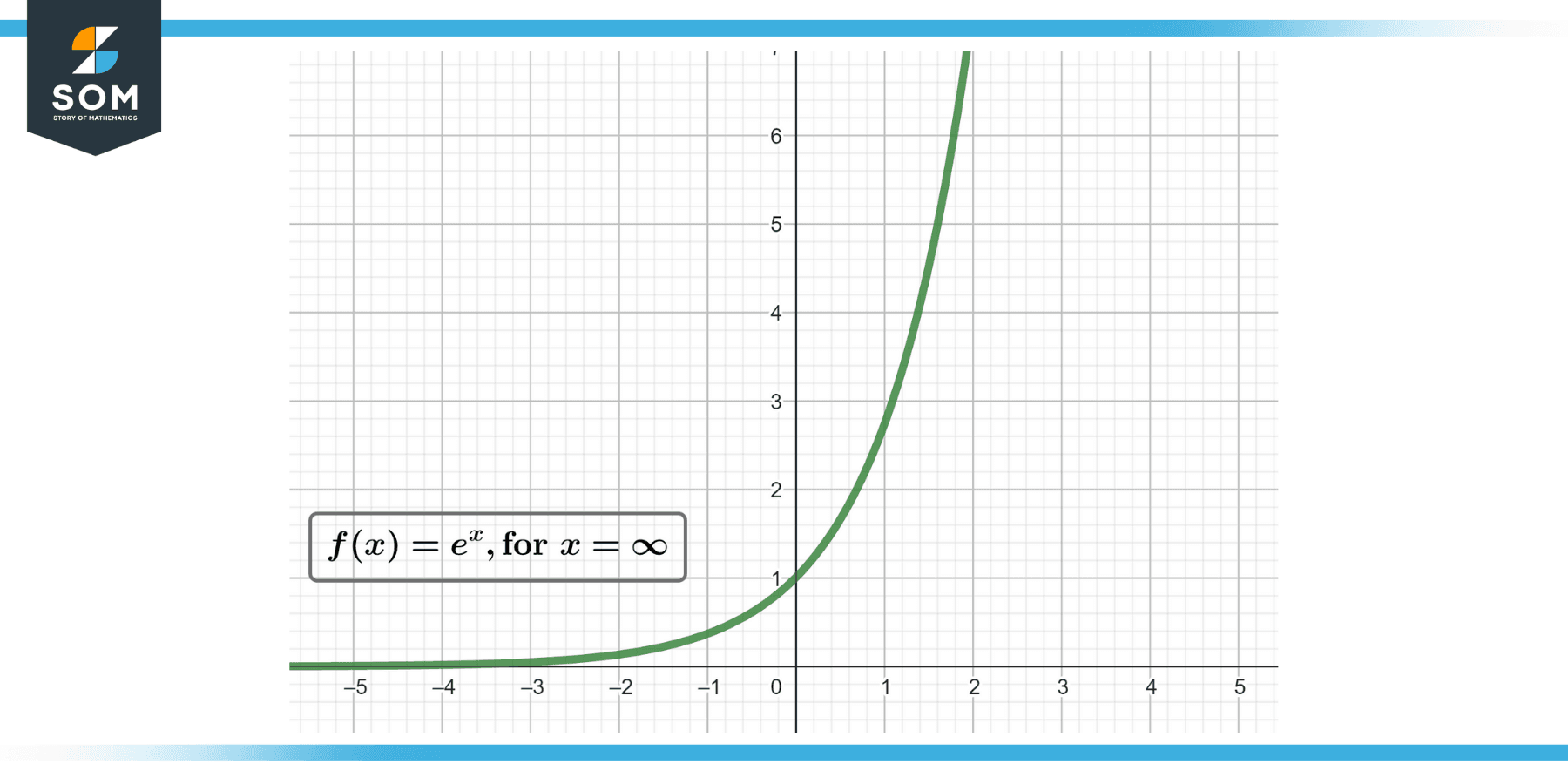
Definition of E to the Negative Infinity
When we say "e to the negative infinity," we are referring to the mathematical expression e^(-∞). This expression simplifies to zero. In mathematical terms:
- e^(-∞) = 0
- This shows that as the exponent approaches negative infinity, the value of the function approaches zero.
Mathematical Calculation of E to the Negative Infinity
Calculating e to the negative infinity involves understanding limits in calculus. The limit can be expressed as follows:
Limit as x approaches -∞ of e^x = 0
This result is significant because it helps us understand the behavior of exponential functions as they decrease. Here’s a breakdown of the calculation:
- As x becomes increasingly negative, e^x approaches zero.
- This is crucial in various applications, especially in decay processes.
Applications in Science
In the realm of science, e to the negative infinity plays a vital role in various fields:
- Physics: Used in decay processes, such as radioactive decay.
- Biology: Models population decline.
- Chemistry: Describes reaction rates.
Financial Applications
In finance, the concept of e to the negative infinity is applied in various ways:
- Present Value Calculations: Helps determine the present value of future cash flows.
- Discounting: Used in discounting cash flows when considering risk over time.
Real World Examples
To illustrate the concept of e to the negative infinity, consider the following examples:
- Investment Growth: If an investment grows exponentially, the value of the investment approaches zero as the interest rate becomes negative.
- Population Decline: A city experiencing a severe decrease in population shows how e to the negative infinity can model this decline.
Conclusion
In summary, e to the negative infinity is a fundamental concept in mathematics with applications in various fields. Understanding this concept can enhance your grasp of exponential functions and their behaviors. We encourage you to explore this topic further and consider how it applies to your field of interest. Please leave your comments or share this article if you found it helpful!
Thank you for reading, and we hope to see you back here for more insightful articles!