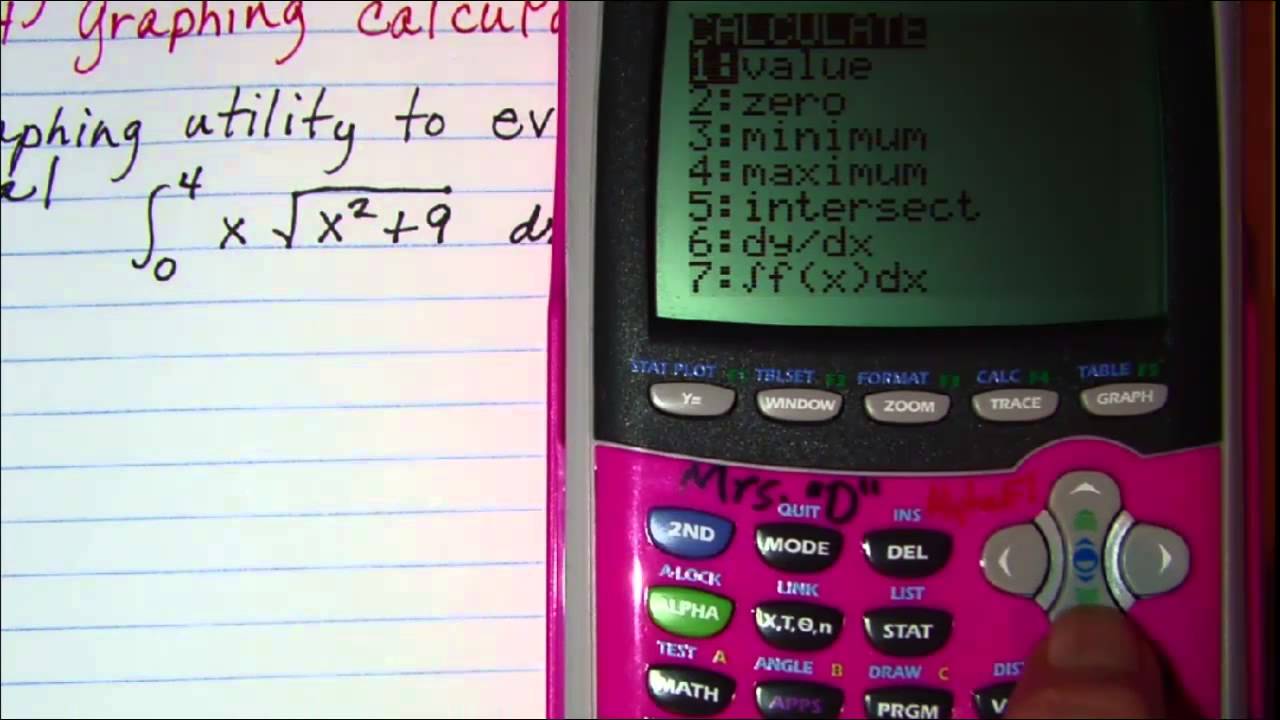Integrating functions using a TI-84 calculator is a skill that many students and professionals seek to master. Whether you're tackling calculus problems for school or need to calculate integrals for your job, knowing how to efficiently use the TI-84 can save you time and enhance your understanding of mathematical concepts. In this article, we will explore step-by-step methods for integrating functions using the TI-84, along with practical examples, tips, and resources that will help you unlock the full potential of your calculator.
With the TI-84's advanced features, integrating functions becomes a much simpler process. You'll learn about the various integration methods available, how to set up your calculator for integration, and the common pitfalls to avoid. Whether you're a beginner or have some experience with the TI-84, this guide will provide valuable insights to help you effectively calculate integrals.
Let's dive into the world of integration with the TI-84 and discover how to make this powerful tool work for you!
Table of Contents
- 1. Introduction to TI-84 Integration
- 2. Setting Up Your TI-84 for Integration
- 3. Types of Integration on TI-84
- 4. Step-by-Step Guide to Integration
- 5. Common Errors to Avoid
- 6. Practical Examples of Integration
- 7. Advanced Integration Techniques
- 8. Additional Resources for Learning
- 9. Conclusion
1. Introduction to TI-84 Integration
The TI-84 calculator is a versatile tool that allows users to perform a wide range of mathematical operations, including integration. Integration is a fundamental concept in calculus that involves finding the accumulated area under a curve defined by a function. Understanding how to integrate can help in various applications, from physics to economics.
2. Setting Up Your TI-84 for Integration
Before you can start integrating, it’s essential to set up your TI-84 correctly. Follow these simple steps:
- Make sure your calculator is turned on.
- Check that your calculator is in the correct mode (usually "Function" mode).
- Clear any previous data or graphs to avoid confusion.
3. Types of Integration on TI-84
There are two primary types of integration you can perform on the TI-84:
- Definite Integration: Calculates the area under a curve within specified limits.
- Indefinite Integration: Finds the general form of the antiderivative of a function.
4. Step-by-Step Guide to Integration
4.1 Performing Definite Integration
To perform definite integration on the TI-84, follow these steps:
- Press the Math button.
- Select the fnInt( function from the menu.
- Input your function, followed by the variable, the lower limit, and the upper limit.
- Press Enter to calculate the integral.
4.2 Performing Indefinite Integration
For indefinite integration, you’ll use a similar approach:
- Press the Math button.
- Select fnInt(.
- Input your function and the variable.
- Press Enter to calculate the antiderivative.
5. Common Errors to Avoid
While using the TI-84 for integration, you may encounter some common errors. Here are a few tips to help you avoid them:
- Always check your syntax before pressing Enter.
- Ensure that you are using the correct variable for integration.
- Double-check your limits for definite integrals.
6. Practical Examples of Integration
To solidify your understanding, let's look at a couple of practical examples:
6.1 Example 1: Definite Integral
Calculate the definite integral of f(x) = x^2 from 1 to 3.
- Input: fnInt(x^2, x, 1, 3)
- Output: 8.66667
6.2 Example 2: Indefinite Integral
Calculate the indefinite integral of f(x) = 3x.
- Input: fnInt(3x, x)
- Output: 1.5x^2 + C
7. Advanced Integration Techniques
For more complex functions, you may need to use advanced techniques:
- Use substitution for composite functions.
- Apply integration by parts for products of functions.
- Utilize numerical methods for functions that cannot be integrated analytically.
8. Additional Resources for Learning
To further enhance your skills, consider the following resources:
9. Conclusion
In this article, we explored how to integrate functions using the TI-84 calculator. We discussed the setup process, types of integration, and provided step-by-step guides for both definite and indefinite integrals. By mastering these techniques, you will enhance your problem-solving skills and gain confidence in using your TI-84.
We encourage you to practice these methods and share your experiences in the comments below. Don't forget to explore other articles on our site for more tips and tricks on mastering your TI-84!
Thank you for reading, and we hope to see you back here soon!