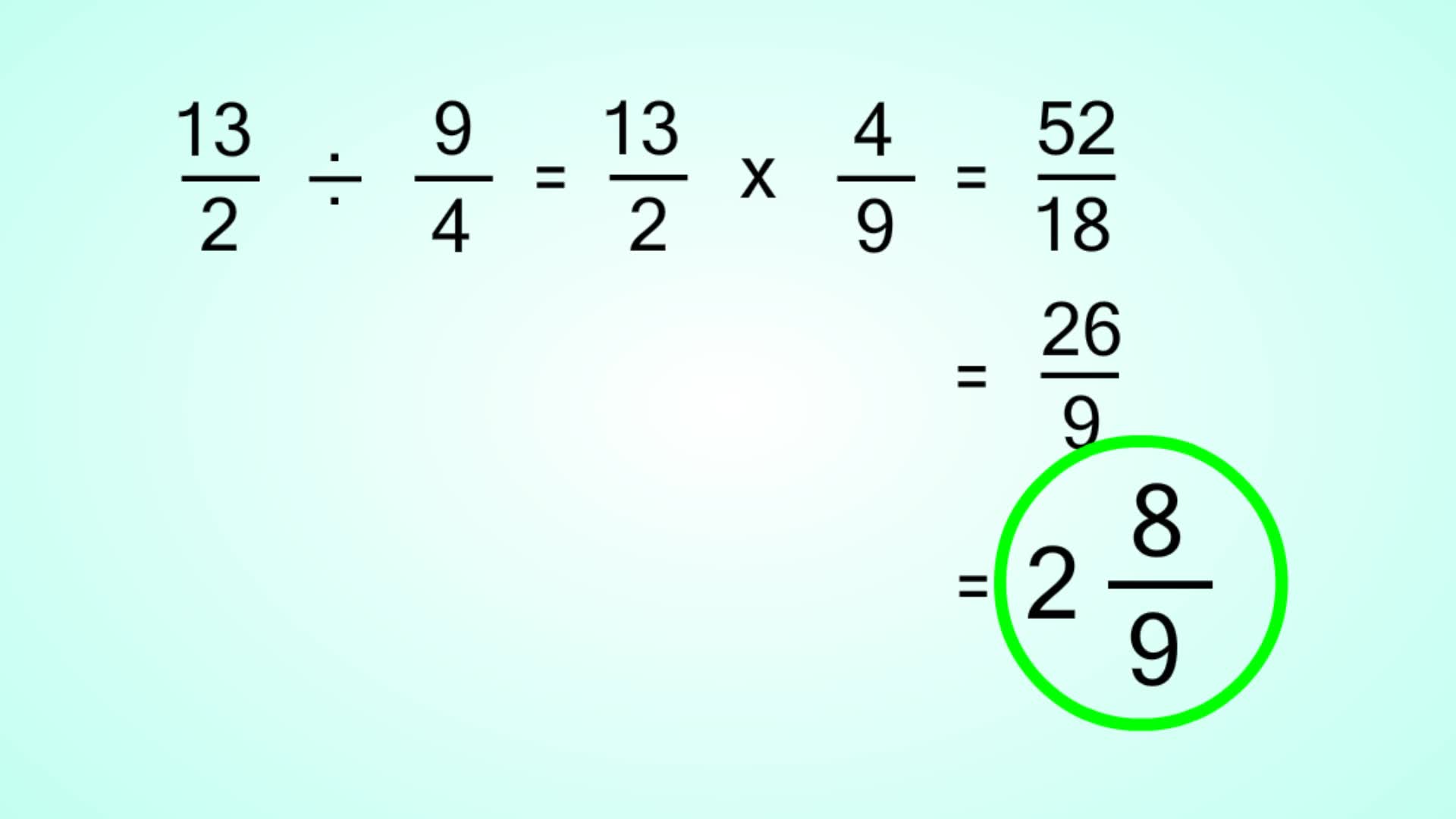Dividing mixed fractions can seem daunting at first, but with the right approach and understanding, it becomes a straightforward process. This guide will walk you through the steps necessary to divide mixed fractions effectively, providing you with the knowledge and skills to tackle similar problems confidently.
In mathematics, mixed fractions consist of a whole number and a proper fraction, making them slightly more complex than regular fractions. However, once you grasp the conversion process and the necessary steps for division, you'll find that dividing mixed fractions is much simpler than it appears. This article will break down the steps, offer helpful tips, and provide practice problems to enhance your understanding.
Whether you are a student looking to improve your math skills or an adult seeking to refresh your knowledge, this article is designed to be a valuable resource. By the end, you'll have a firm grasp on how to divide mixed fractions and be prepared to tackle any related challenges you may encounter.
Table of Contents
- Understanding Mixed Fractions
- Steps to Divide Mixed Fractions
- Converting Mixed Fractions to Improper Fractions
- Dividing Improper Fractions
- Simplifying Fractions
- Practice Problems
- Common Mistakes to Avoid
- Conclusion
Understanding Mixed Fractions
Mixed fractions are composed of two parts: a whole number and a fraction. For example, 2 1/3 is a mixed fraction where 2 is the whole number and 1/3 is the proper fraction. Understanding how to work with these fractions is vital for performing arithmetic operations, including division.
Key Characteristics of Mixed Fractions
- Consist of a whole number and a proper fraction.
- Can be converted into improper fractions for easier calculations.
- Used in various real-life situations, such as cooking and construction.
Steps to Divide Mixed Fractions
To divide mixed fractions, follow these systematic steps:
- Convert the mixed fractions to improper fractions.
- Change the division operation to multiplication by the reciprocal of the second fraction.
- Multiply the numerators and denominators.
- Simplify the result if possible.
Converting Mixed Fractions to Improper Fractions
To convert a mixed fraction to an improper fraction, follow these steps:
- Multiply the whole number by the denominator of the fraction.
- Add the numerator of the fraction to the result from step one.
- Place this result over the original denominator.
For example, to convert 2 1/3 to an improper fraction:
- 2 (whole number) × 3 (denominator) = 6
- 6 + 1 (numerator) = 7
- Thus, 2 1/3 = 7/3
Dividing Improper Fractions
Once you have converted mixed fractions to improper fractions, you can proceed with division.
For example, dividing 2 1/3 by 1 1/2:
- Convert 2 1/3 to 7/3 and 1 1/2 to 3/2.
- Change the division to multiplication: 7/3 ÷ 3/2 becomes 7/3 × 2/3.
- Multiply the numerators: 7 × 2 = 14.
- Multiply the denominators: 3 × 3 = 9.
- The result is 14/9, which can be simplified to 1 5/9.
Simplifying Fractions
Simplifying fractions involves reducing the fraction to its lowest terms. This can be done by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by that number.
- For 14/9, the GCD is 1. Thus, it is already in its simplest form.
- For improper fractions that can be converted back to mixed fractions, divide the numerator by the denominator.
Practice Problems
To sharpen your skills, try solving these problems:
- Divide 3 1/4 by 2 2/5.
- Divide 1 1/2 by 2/3.
- Divide 5 3/8 by 1 1/4.
Common Mistakes to Avoid
Here are some frequent pitfalls to avoid when dividing mixed fractions:
- Forgetting to convert mixed fractions to improper fractions.
- Incorrectly changing division to multiplication by the reciprocal.
- Not simplifying the final answer.
Conclusion
Dividing mixed fractions can be easily mastered with practice and understanding. By converting mixed fractions to improper fractions, changing division to multiplication, and simplifying your results, you can confidently tackle any problem involving mixed fractions.
Remember to practice regularly to reinforce your skills. If you have questions or need further clarification, feel free to leave a comment or explore additional resources on this topic.
Call to Action
If you found this guide helpful, please consider sharing it with others or leaving a comment below. For more articles and resources to enhance your math skills, be sure to browse our other content!
Thank you for reading, and we hope to see you again soon!