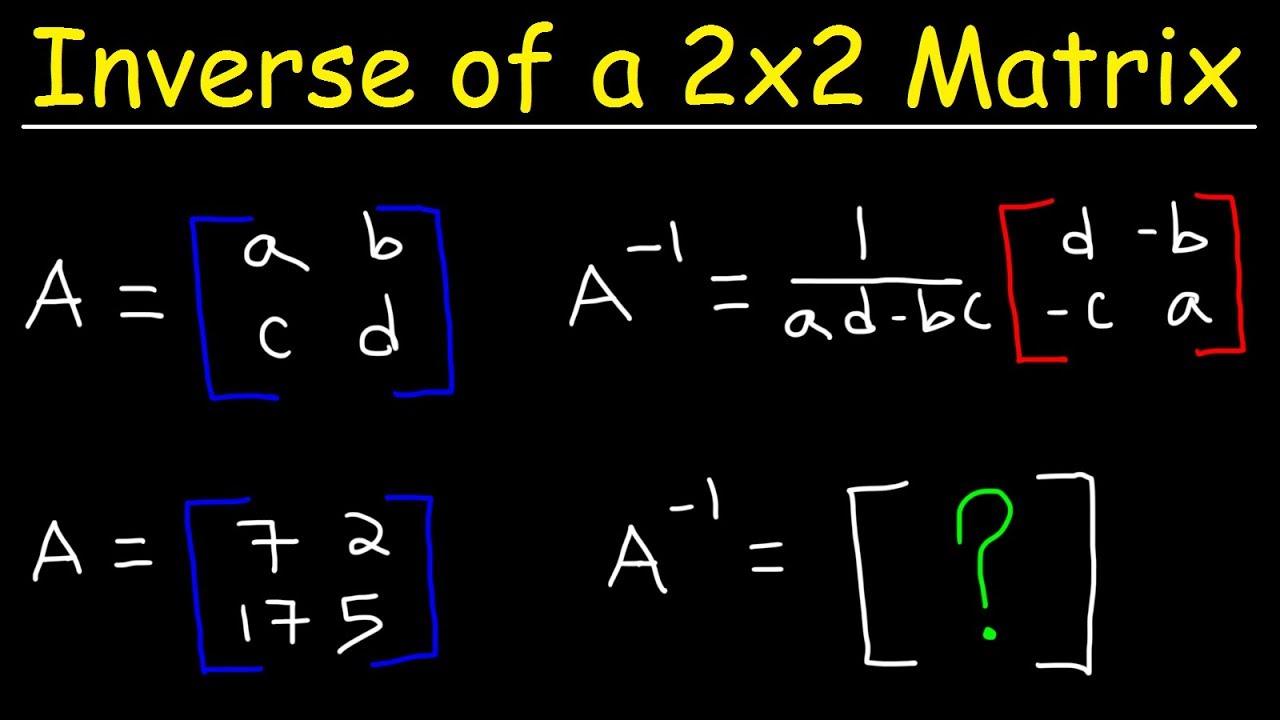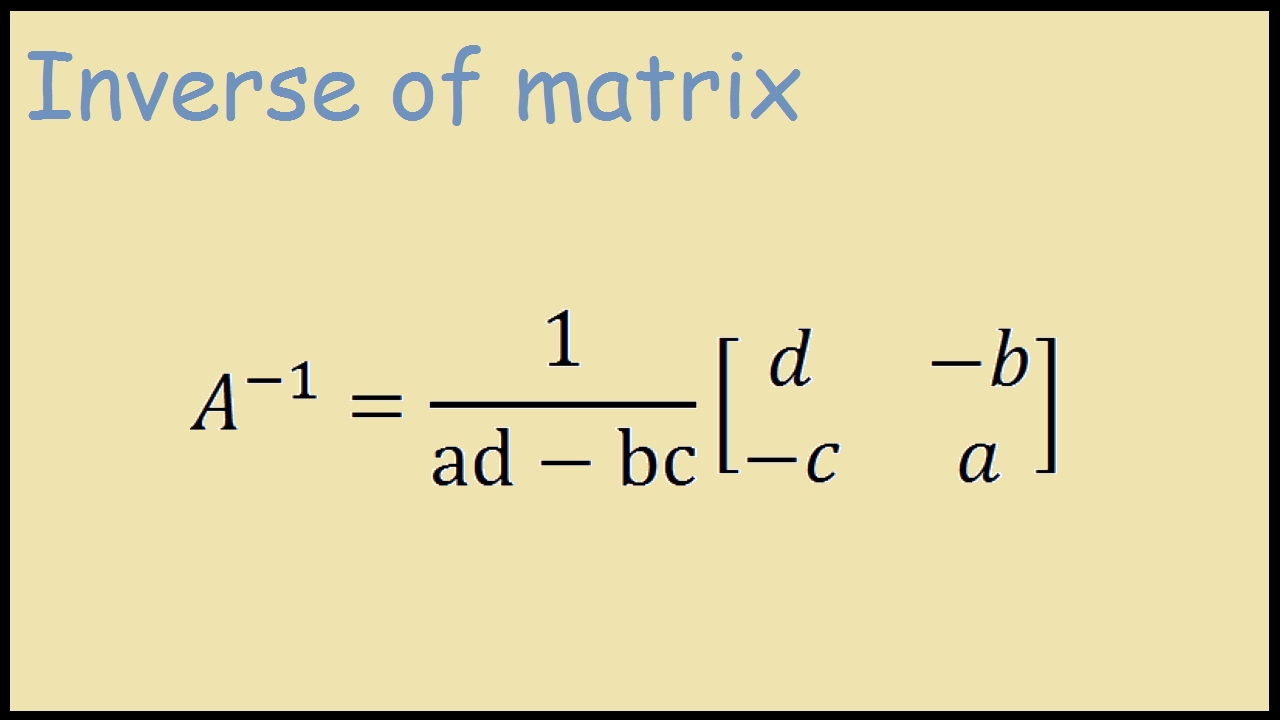Understanding how to find the inverse of a 2x2 matrix is an essential skill in linear algebra. Inverse matrices are pivotal in solving systems of linear equations, performing transformations in geometry, and many applications in both mathematics and engineering. In this article, we will delve into the methods for calculating the inverse of a 2x2 matrix, explore its applications, and provide insightful examples to solidify your understanding.
In linear algebra, the inverse of a matrix is analogous to the reciprocal of a number. When a matrix has an inverse, it is referred to as non-singular or invertible, and the existence of this inverse is determined by the determinant of the matrix. This article will guide you through the process of finding the inverse of a 2x2 matrix step by step, ensuring clarity and comprehension of the topic.
Whether you are a student learning linear algebra or a professional needing to refresh your knowledge, this guide is designed to equip you with the necessary tools and understanding. By the end of this article, you will be able to confidently calculate the inverse of any 2x2 matrix and understand its significance in various applications.
Table of Contents
- Understanding Matrices
- What is an Inverse Matrix?
- Conditions for Inverses
- How to Find Inverse of 2x2 Matrix
- Step-by-Step Example
- Applications of Inverse Matrix
- Common Mistakes in Inverse Calculation
- Conclusion
Understanding Matrices
A matrix is a rectangular array of numbers arranged in rows and columns. For example, a 2x2 matrix has two rows and two columns, represented as:
A = [[a, b], [c, d]]
Here, a, b, c, and d are elements of the matrix. Matrices are widely used in mathematical calculations, computer science, statistics, and engineering.
What is an Inverse Matrix?
The inverse of a matrix A is denoted as A-1. The defining property of the inverse is that when a matrix is multiplied by its inverse, the result is the identity matrix. For a 2x2 matrix, this can be expressed as:
A * A-1 = I
Where I is the identity matrix, which for a 2x2 matrix is:
I = [[1, 0], [0, 1]]
Conditions for Inverses
Not every matrix has an inverse. A matrix is invertible if:
- The determinant of the matrix is non-zero.
- The matrix is square (same number of rows and columns).
For a 2x2 matrix, the determinant is calculated as:
det(A) = ad - bc
How to Find Inverse of 2x2 Matrix
To find the inverse of a 2x2 matrix, you can use the following formula:
If A = [[a, b], [c, d]], then:
A-1 = (1/det(A)) * [[d, -b], [-c, a]]
Provided that det(A) ≠ 0.
Step 1: Calculate the Determinant
First, calculate the determinant of the matrix using the formula det(A) = ad - bc.
Step 2: Apply the Inverse Formula
Once the determinant is found, substitute the values into the inverse formula to find A-1.
Step-by-Step Example
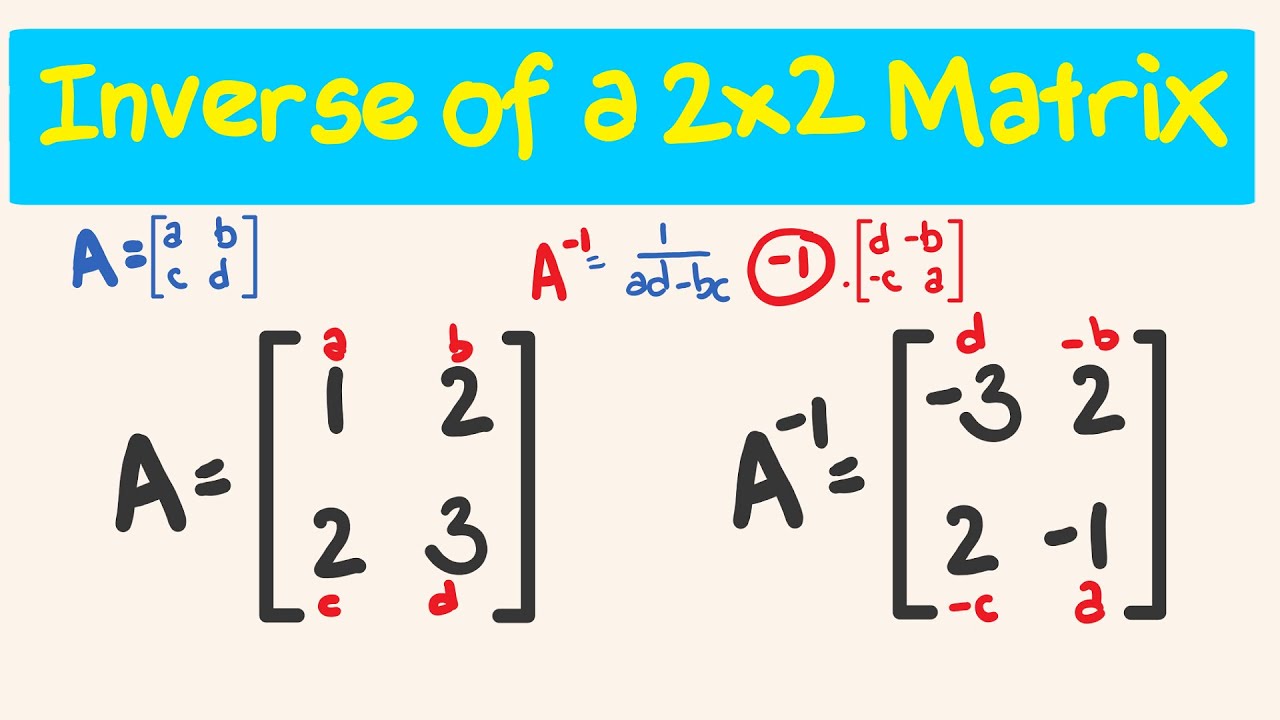
Let’s consider an example with the matrix:
A = [[4, 3], [2, 1]]
Step 1: Calculate the Determinant
Using the formula:
det(A) = (4)(1) - (3)(2) = 4 - 6 = -2
Step 2: Apply the Inverse Formula
Since the determinant is non-zero, we can find the inverse:
A-1 = (1/-2) * [[1, -3], [-2, 4]]
This simplifies to:
A-1 = [[-0.5, 1.5], [1, -2]]
Applications of Inverse Matrix
The inverse of a matrix has numerous applications, including:
- Solving systems of linear equations using the formula
X = A-1B. - Computer graphics transformations.
- Statistical analyses, such as in regression analysis.
- Control systems in engineering.
Common Mistakes in Inverse Calculation
While calculating the inverse of a matrix, some common mistakes include:
- Forgetting to check if the determinant is non-zero.
- Incorrectly applying the inverse formula.
- Arithmetic errors during calculations.
Conclusion
In this article, we have explored the process of finding the inverse of a 2x2 matrix, the conditions for the existence of an inverse, and its applications. Understanding the inverse of matrices is crucial for various fields in mathematics and engineering. We encourage you to practice finding inverses with different matrices to enhance your skills. If you have any questions or wish to share your insights, feel free to leave a comment below or explore other articles on our site!
References
- Linear Algebra and Its Applications by Gilbert Strang
- Introduction to Linear Algebra by Daniel C. Lay
- Matrix Algebra Useful for Statistics by David A. Harville