The Pythagorean theorem is one of the most fundamental results in mathematics, and Euclid’s proof of this theorem remains a cornerstone of geometric understanding. This ancient theorem, which relates the sides of a right triangle, has been studied and employed for thousands of years. In this article, we will explore Euclid's proof of the Pythagorean theorem in detail, examining its historical context, methodology, and implications for modern mathematics.
Understanding the Pythagorean theorem is essential not only for students of mathematics but also for professionals in fields ranging from architecture to engineering. By the end of this article, readers will gain a comprehensive understanding of Euclid's proof, its significance, and how it has influenced mathematical thought throughout history.
This article is structured to provide a clear and thorough examination of the topic. We will begin with a historical overview, followed by an explanation of the theorem itself and Euclid's proof. We will then delve into applications of the theorem, conclude with key takeaways, and provide resources for further learning.
Table of Contents
- Historical Overview of the Pythagorean Theorem
- Understanding the Pythagorean Theorem
- Euclid's Proof of the Pythagorean Theorem
- Applications of the Theorem
- Significance in Modern Mathematics
- Conclusion
- Resources for Further Learning
Historical Overview of the Pythagorean Theorem
The Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides (a² + b² = c²), has a rich history. The theorem is named after the ancient Greek mathematician Pythagoras, who lived around 570-495 BCE. However, the theorem was known to mathematicians in various cultures long before Pythagoras, including the Babylonians and Indians.
Euclid, often referred to as the "father of geometry," made significant contributions to mathematics in his work "Elements," written around 300 BCE. In this work, Euclid systematically compiled and organized the knowledge of geometry known at the time, including the Pythagorean theorem and its proof. His approach established a standard for mathematical rigor and logical reasoning that would influence centuries of mathematical thought.
Euclid's proof of the Pythagorean theorem is notable for its clarity and logical structure, using only geometric constructions and properties. This method not only demonstrated the truth of the theorem but also exemplified the deductive reasoning that is foundational to mathematics.
Understanding the Pythagorean Theorem
To fully grasp Euclid's proof, it is essential to understand the components of the Pythagorean theorem. A right triangle consists of three sides: the hypotenuse (c), which is the longest side opposite the right angle, and the two legs (a and b), which form the right angle. The Pythagorean theorem asserts that:
- Hypotenuse (c): The longest side of the triangle.
- Leg a: One of the two sides forming the right angle.
- Leg b: The other side forming the right angle.
Mathematically, the theorem can be expressed as:
a² + b² = c²
This equation allows for the calculation of the length of any side of a right triangle, provided the lengths of the other two sides are known. The theorem's applications extend beyond pure mathematics, influencing various fields such as physics, engineering, and architecture.
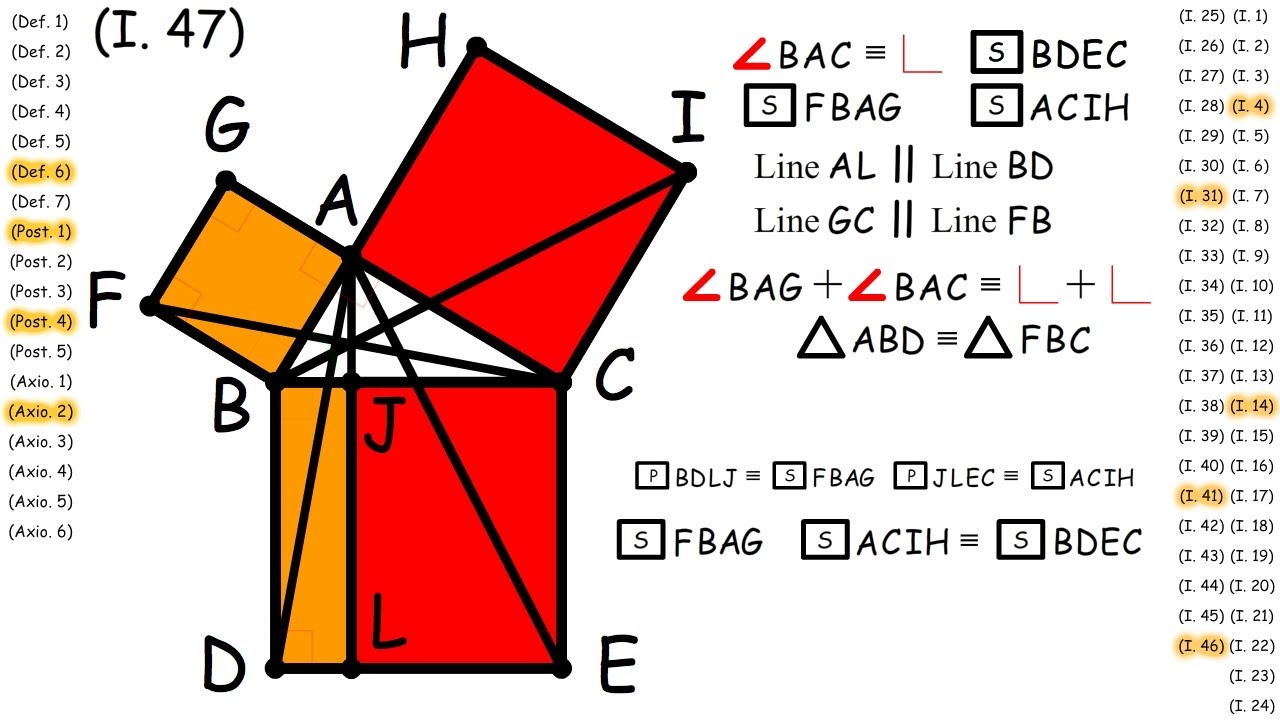
Euclid's Proof of the Pythagorean Theorem
Euclid's proof of the Pythagorean theorem is a brilliant geometric demonstration that relies on the construction of squares on each side of the triangle. Below, we will explore the proof in detail, divided into two main sections: the geometric approach and the algebraic interpretation.
The Geometric Approach
Euclid's proof begins with a right triangle ABC, where angle C is the right angle. To demonstrate the theorem, Euclid constructs squares on each of the triangle's three sides:
- Square on side a (Area = a²)
- Square on side b (Area = b²)
- Square on side c (Area = c²)
Euclid then shows that the area of the larger square (on the hypotenuse) is equal to the combined areas of the two smaller squares (on the legs). He does this through a series of geometric constructions that rearrange the areas of the squares, illustrating that:
Area of square on side c = Area of square on side a + Area of square on side b
Thus, he concludes that:
c² = a² + b²
The Algebraic Interpretation
While Euclid's proof is fundamentally geometric, it can also be interpreted algebraically. By applying algebraic methods to the geometric relationships established in the proof, we can express the theorem in a form that is familiar in modern mathematics.
By rearranging the equation derived from the geometric proof, we can isolate the terms to demonstrate the equality:
- Start with the equation from the geometric proof:
- c² = a² + b²
- Rearranging gives us the standard form of the theorem.
This algebraic interpretation connects Euclid's geometric reasoning with modern mathematical practices, illustrating the theorem's timeless relevance.
Applications of the Theorem
The Pythagorean theorem is not merely a theoretical construct; it has practical applications across various fields. Some notable applications include:
- Architecture: Ensuring structures are built with right angles for stability.
- Navigation: Calculating distances between points on a map using right triangles.
- Physics: Analyzing forces and motion where right angles occur.
- Computer Graphics: Rendering 3D images and calculating distances between objects.
These applications highlight the theorem's significance in both theory and practice, demonstrating its enduring importance in our daily lives.
Significance in Modern Mathematics
Euclid's proof of the Pythagorean theorem laid the groundwork for the development of modern geometry. His methodical approach and emphasis on logical reasoning set a standard for mathematical proofs that persists today. The theorem continues to be a fundamental part of mathematics education, serving as an introduction to geometric principles and proof techniques.
Moreover, the Pythagorean theorem has inspired countless mathematicians throughout history, leading to further developments in geometry, trigonometry, and algebra. Its implications extend into various branches of mathematics, influencing theories and applications in fields such as calculus and topology.
Conclusion
In conclusion, Euclid's proof of the Pythagorean theorem is a remarkable achievement in the history of mathematics. By providing a clear and logical demonstration of this fundamental relationship in geometry, Euclid established a framework for mathematical reasoning that remains relevant today. Understanding this proof not only enhances our appreciation for geometry but also highlights the interconnectedness of mathematical concepts.
We invite readers to explore this topic further, engage with the mathematical community, and consider how the Pythagorean theorem applies in various fields. Please leave your comments, share this article, or check out additional resources on our site.
Resources for Further Learning
For those interested in delving deeper into the topic, here are some recommended resources:
- Khan Academy: Right Triangles and the Pythagorean Theorem
-

Euclids Pythagorean Theorem Proof Remix Permaclip
(I.47) Pythagorean Theorem, Euclid's Proof YouTube

Euclid S Proof Of The Pythagorean Theorem