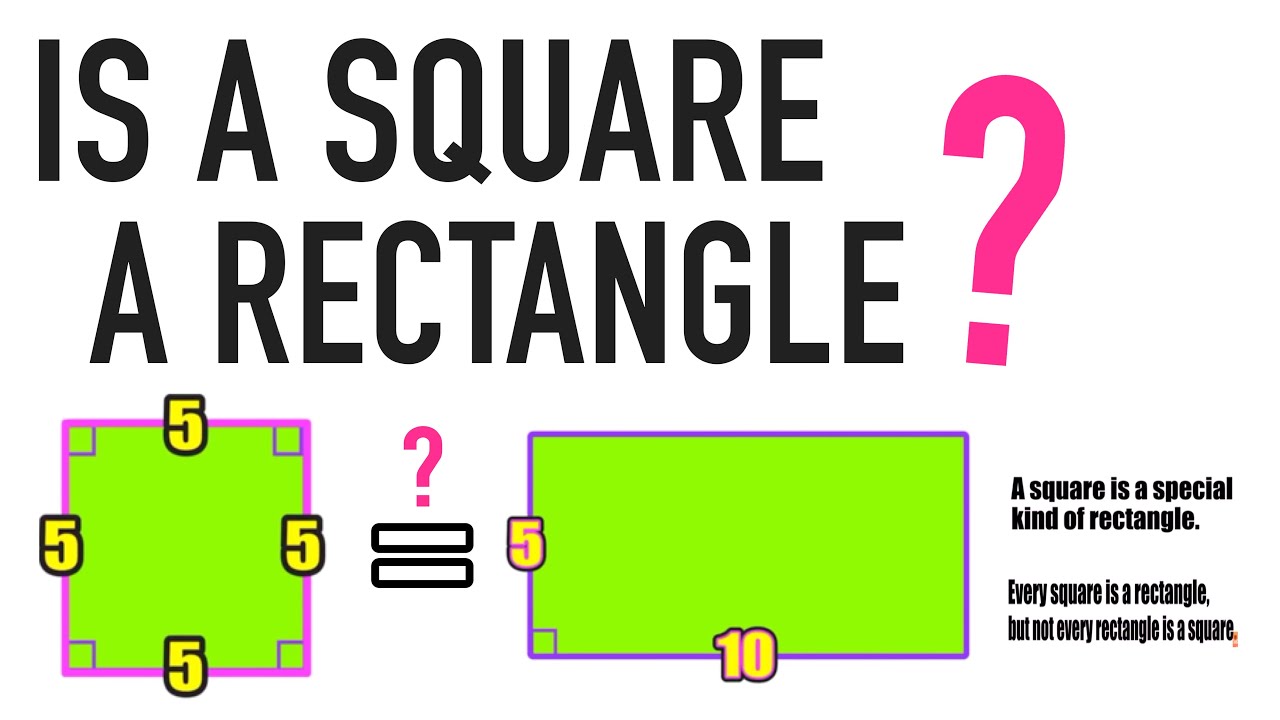When it comes to geometry, one of the most common questions asked is, "Is a rectangle a square?" This question often arises in both academic settings and everyday life situations. Understanding the relationship between rectangles and squares is essential for students, educators, and anyone interested in mathematics. In this article, we will explore the definitions, properties, and differences between rectangles and squares, providing clarity on this often-confused topic.
The terms "rectangle" and "square" are frequently used in geometry, but they refer to specific types of quadrilaterals. A rectangle is defined as a quadrilateral with opposite sides that are equal in length and four right angles, while a square is a special type of rectangle that has all four sides equal in length. This fundamental difference is crucial for understanding their relationship.
Throughout the following sections, we will delve deeper into the characteristics of rectangles and squares, examine their properties, and clarify why not all rectangles are squares, while all squares can indeed be classified as rectangles. So, let’s embark on this geometric journey to unravel the complexities of shapes!
Table of Contents
- Definition of Rectangles and Squares
- Properties of Rectangles
- Properties of Squares
- Key Differences Between Rectangles and Squares
- Examples of Rectangles and Squares
- Real-World Applications
- Visualizing Rectangles and Squares
- Conclusion
Definition of Rectangles and Squares
A rectangle is a four-sided polygon (quadrilateral) with the following attributes:
- Opposite sides are equal in length.
- All four angles are right angles (90 degrees).
- The diagonals of a rectangle are equal in length and bisect each other.
In contrast, a square is a specific type of rectangle characterized by:
- All four sides are equal in length.
- All four angles are right angles (90 degrees).
- The diagonals of a square are equal in length and bisect each other at right angles.
Properties of Rectangles
Rectangles have several important properties that distinguish them as a unique shape:
- Area: The area of a rectangle can be calculated using the formula: Area = length × width.
- Perimeter: The perimeter is calculated as: Perimeter = 2(length + width).
- Diagonals: The diagonals of a rectangle can be found using the Pythagorean theorem, as they form right triangles.
Diagram of a Rectangle
Below is a simple representation of a rectangle:
[INSERT DIAGRAM OF RECTANGLE HERE]
Properties of Squares
Squares possess all the properties of rectangles but with additional constraints:
- Area: The area of a square is calculated as: Area = side × side.
- Perimeter: The perimeter is calculated as: Perimeter = 4 × side.
- Diagonals: The diagonals of a square are equal and can also be calculated using the formula: Diagonal = side × √2.
Diagram of a Square
Below is a simple representation of a square:
[INSERT DIAGRAM OF SQUARE HERE]
Key Differences Between Rectangles and Squares
While all squares are rectangles, not all rectangles are squares. Here are the key differences:
- Side Length: In a square, all four sides are equal, whereas, in a rectangle, opposite sides are equal but adjacent sides can be of different lengths.
- Specificity: Squares are a specific subset of rectangles with stricter requirements.
- Symmetry: Squares exhibit more symmetry compared to rectangles, which can be skewed in shape.
Examples of Rectangles and Squares
Consider the following examples to illustrate the differences:
- A typical door is often a rectangle, with two sides being longer than the other two.
- A chessboard is a classic example of a square, with each side being equal.
Real-World Applications
Understanding the difference between rectangles and squares is essential in various fields, including:
- Architecture: Designing buildings often involves the use of both shapes.
- Art: Creating patterns can require knowledge of these geometric properties.
- Engineering: Many mechanical parts are designed based on these shapes for functionality and efficiency.
Visualizing Rectangles and Squares
To better understand these shapes, visualizations can be helpful. Consider using graph paper or digital tools to sketch different rectangles and squares, comparing their properties visually.
Conclusion
In conclusion, while the question "Is a rectangle a square?" may seem simple, it opens up a broader discussion about geometry and the properties of shapes. We have established that all squares are rectangles, but not all rectangles meet the criteria to be classified as squares. Understanding these distinctions is critical for students and professionals alike.
We encourage you to share your thoughts in the comments below, and if you found this article helpful, please consider sharing it with others interested in geometry!
Thank you for reading, and we look forward to seeing you again for more insightful discussions on mathematics and geometry!